结构分析:
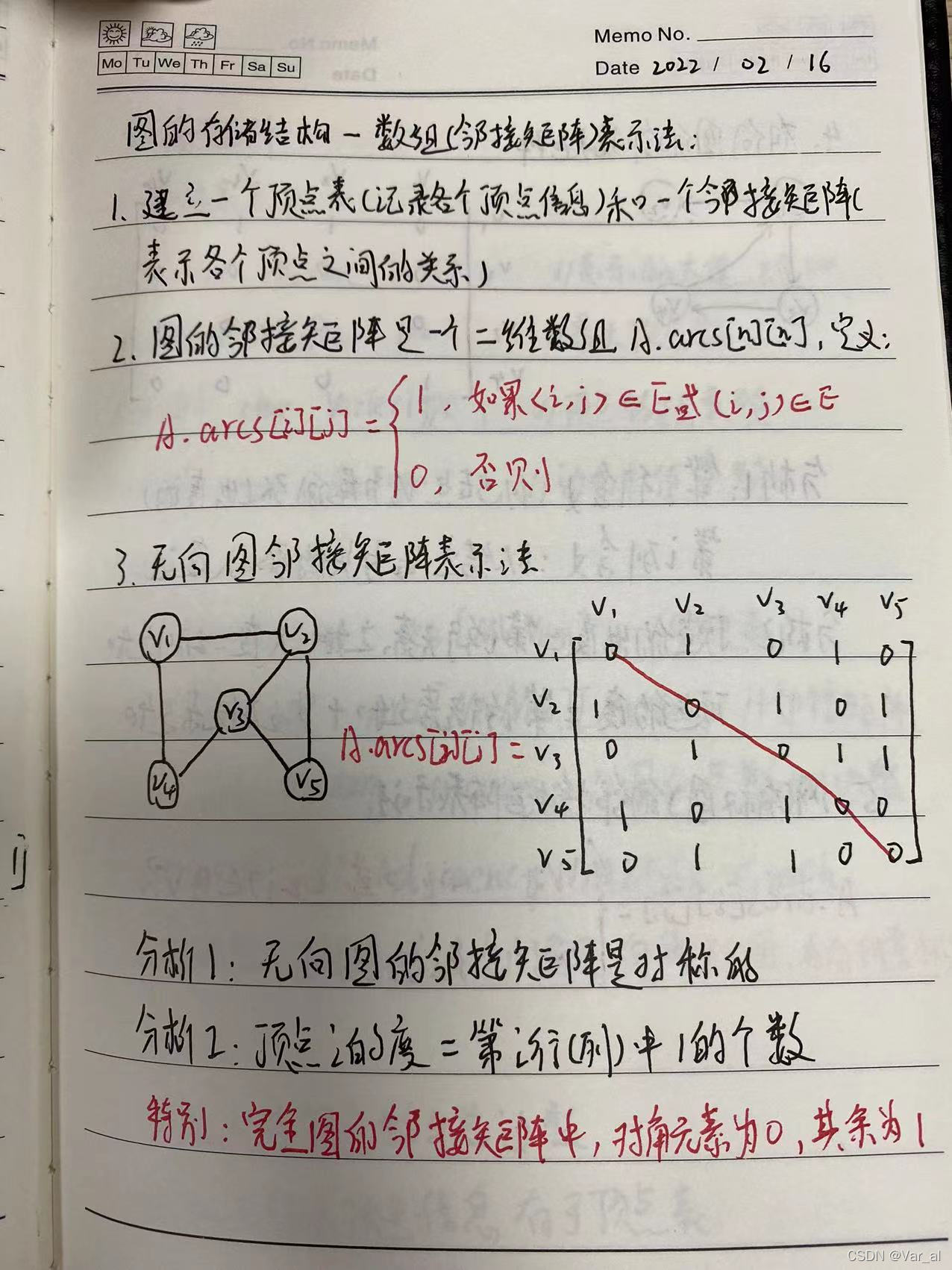
邻接矩阵 |
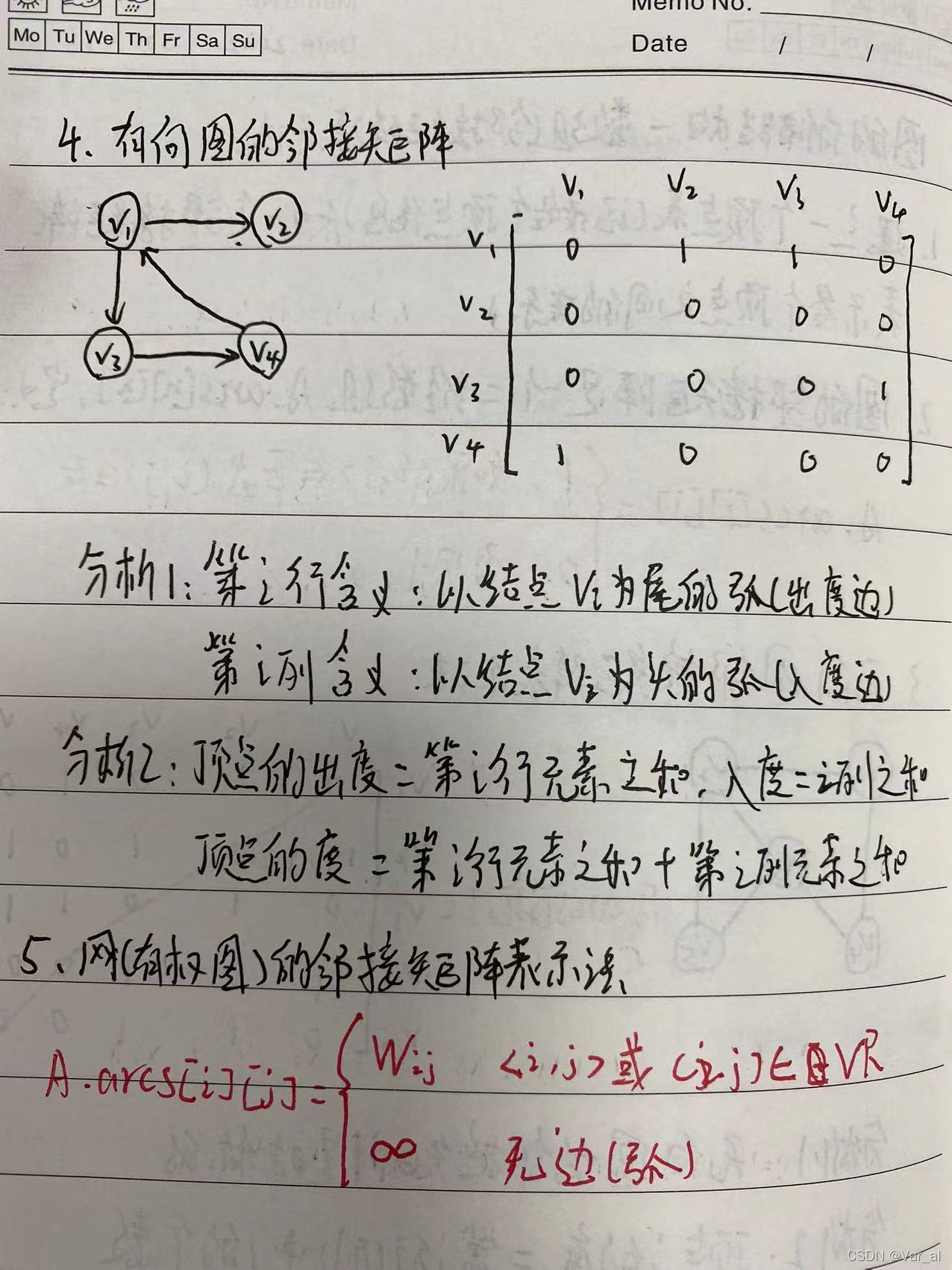
邻接矩阵 |
算法思想:
- 输入总顶点数和总边数
- 一次输入顶点休息存于顶点表
- 初始化邻接矩阵,每个权值为极大值
- 构造邻接矩阵
存储表示:
#define MaxInt 32767 // 极大值
#define MVNum 100 // 最大定点数
typedef char VerTexType;// 顶点数据类型
typedef int ArcType; // 边的权值类型
// 图的结构定义
typedef struct
{
VerTexType vexs[MVNum]; // 顶点表
ArcType arcs[MVNum][MVNum]; // 邻接矩阵
int vexnum, arcnum; // 图的顶点数和边数
}AMGraph;
算法实现:
// 采用邻接矩阵表示法创建无向网
Status CreateUDN(AMGraph &G)
{
// 输入总顶点数与总边数
cin >> G.vexnum >> G.arcnum;
// 输入顶点消息于顶点表
for (int i = 0; i < G.vexnum; ++i)
cin >> G.vexs[i];
// 初始化邻接矩阵,每个权值为极大值
for (int i = 0; i < G.vexnum; ++i)
for (int j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = MaxInt;
// 构造邻接矩阵
for (int k = 0; k < G.vexnum; ++k)
{
char v1, v2, w;
cin >> v1 >> v2 >> w;
int i = LocateVex(G, v1);
int j = LocateVex(G, v2);
G.arcs[i][j] = w; G.arcs[j][i] = w;
}
return 0;
}
//顶点在顶点表中的下标
int LocateVex(AMGraph G, VerTexType u)
{
int i;
for (int i = 0; i < G.vexnum; ++i)
if (u == G.vexs[i]) return i;
return -1;
}
邻接矩阵优缺点:
- 优点:
- 直观、简单、好理解
- 方便检查任意两点间是否有边
- 方便找任一顶点的所有邻接点
- 方便 计算顶点的度 - 缺点
- 不利于增删顶点
- 浪费空间-稀疏图(点多边少)有大量无效元素,但对稠密图(完全图)还是很合算的
- 浪费时间-统计图中共有多少条边 - 存储空间为O(n²)